Średnia, można powiedzieć, że jest to najprostszy model jaki możemy zbudować w statystyce. Średnia jako model zbiera wszystkie przypadki (obserwacje).
Jest ona wartością hipotetyczną, która jest obliczana na podstawie wszystkich obserwacji zawartych w zbiorze danych. Po obliczeniu średniej możemy zastanowić się czy nasz model jest dobrze dopasowany do danych znajdujących się w zbiorze. Musimy więc sprawdzić różnice między naszym modelem (średnią) i danymi zawartymi w zbiorze.
Przykład:
Mamy uczniów, którzy zdawali egzamin gimnazjalny. Liczba punktów otrzymana przez każdego z nich to: 54, 68, 90, 65, 88, 67.
Średnia punktów wynosi X=54+68+90+65+88+67/6 = 72
Czy średnia liczba punktów (762) uzyskana z egzaminu gimnazjalnego dobrze oddaje tendencje występującą w danych?
Policzmy najpierw musimy odjąć wynik od średniej 54-72=-18
Policzmy sumę wszystkich różnic czyli całkowity błąd ∑=Xi-X = (54-72)+(68-72)+(90-72)+(65-72)+(88-72)+(67-72)=(-18)+(-4)+18+(-7)+16+(-5)=0
Na wykresie linią poziomą oznaczono średnią, granatowe kropki to punkty z egzaminu poszczególnych uczniów, a kreski łączące średnią z punktami to różnice między średnią a liczbą punktów poszczególnych uczniów. Inaczej mówiąc jest to różnica między naszym modelem a danymi w zbiorze.
Sprawdźmy:
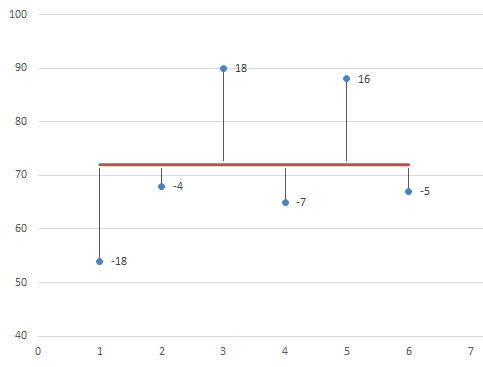
Widzimy, że błąd wynosi zero, czyli, że mamy idealne dopasowanie modelu do danych, ale niestety nie jest to prawda, ponieważ mamy wyniki, które się znoszą, są wyniki ujemne, są też dodatnie, i zawsze wynik, który otrzymamy będzie wynosił 0.
Cóż wiec zrobić? Statystycy wpadli na pomysł, że trzeba pozbyć się ujemnych znaków z równania. Co zaś powoduje usunięcie znaku ujemnego? Podniesienie wyrażenia czyli sumy różnic, błędów do kwadratu.
Suma błędów podniesiona do kwadratu ∑=(X1-X)2
(54-72)2+(68-72)2+(90-72)2+(65-72)2+(88-72)2+(67-72)2=(-18)2+(-4)2+182+(-7)2+162+(-5)2=324+16+324+49+256+25=994
Suma kwadratów błędów (SS) wynosi 994. Jednak pojawia się tutaj taki kłopot, że im więcej danych mamy, tym wyższy będzie błąd sum kwadratów. Dlatego też dzielimy całą sumę kwadratów przez liczbę obserwacji minus 1 – gdyż chcemy oszacować błąd w populacji (otrzymujemy wówczas wariancję).
Wariancja s2=994/6-1 = 199
Taki wynik można zinterpretować, że średni błąd w naszych danych wynosi 199 punktów w jednostkach kwadratowych
Aby pozbyć się kwadratów, które nam były potrzebne aby pozbyć się znaków ujemnych z równania, należy wynik wziąć pod pierwiastek kwadratowy i uzyskamy wówczas odchylenie standardowe.
Odchylenie standardowe wynosi =14,11
Odchylenie standardowe jest więc miarą dopasowania modelu do danych. Czyli mówi nam jak dobrze model odzwierciedla (jest dopasowany) dane.
Małe odchylenie standardowe mówi, że model jest dobrze dopasowany do danych, natomiast duże odchylenie standardowe mówi, że model niezbyt dobrze odzwierciedla dane (względem średniej).
Odchylenie standardowe równe 0 oznacza, że wszystkie wyniki są takie same.
Cóż więc z naszym modelem. Otóż jeżeli dane nie są dobrze dopasowane do danych średnia jest złym przybliżeniem wyników w zbiorze i należy posłużyć się inną miarą. Jeżeli natomiast średnia dobrze obrazuje to co się dzieje w zbiorze danych wówczas można się na nią powoływać.
Dobrze dopasowany model do danych daje dobre przybliżenie tego co się dzieje w rzeczywistości, natomiast, jeżeli dopasujemy do danych nieprawidłowy model, wówczas nie będziemy mieli prawidłowego przybliżenia tego co się dzieje w rzeczywistości i w związku z tym wyniki, które sobie policzymy będą nieprawidłowe. Dlatego ważne jest aby dobrze dopasować model czyli wybrać taki, który będzie dobrze dopasowany do naszych danych.
Generalnie, jeżeli chodzi o modele w statystyce to każdy z nich można sprowadzić do równania
Wynik = model + błąd.
