Test chi2 jest generalnie wykorzystywany do badania współzależności dwóch zmiennych.
Poròwnuje dwie zmienne w tabeli kontyngencji, aby sprawdzić czy różnią się od siebie.
Kiedy stosować test chi2 ?
Test chi2 nie wymaga założeń o normalności rozkładu czy jednorodności wariancji. Można za jego pomocą analizować zmienne nominalne i porządkowe.
Testujemy, czy liczebności empiryczne (obserwowane), czyli otrzymane z badania, różnią się istotnie od oczekiwanych czyli teoretycznych. Liczebności oczekiwane powinny być większe od 5.
Hipoteza zerowa H0 mówi, że badane zmienne są niezależne.
Hipoteza alternatywna H1 mówi, że istnieje związek między badanymi zmiennymi.
Dla zmiennych powinno się zbudować tabelę dwudzielczą.
Tabela dwudzielcza jest zbudowana z dwóch zmiennych, które mają po dwie wartości, np. zmienna płeć ma dwie wartości: mężczyzna i kobieta.
Najpierw należy postawić sobie pytanie badawcze i hipotezę badawczą.
My zbadamy sobie związek między płcią a stosowaniem kremu na zmarszczki.
Pytanie badawcze, które sobie postawimy, jest następujące: Czy mężczyźni różnią się od kobiet w stosowaniu kremu na zmarszczki.
Tabela zawierająca liczebności empiryczne, czyli te, które pochodzą z badań, wygląda następująco:
Liczebności empiryczne
| Płeć | Stosowanie kremu na zmarszczki | Ogółem | |
|---|---|---|---|
| Nie | Tak | ||
| Mężczyzna | 36 | 80 | 116 |
| Kobieta | 16 | 110 | 126 |
| Ogółem | 52 | 190 | 242 |
Następnie wylicza się wartości oczekiwane dla każdej komórki tabeli dwudzielczej wg wzoru:
Po podstawieniu danych:
Tabela zawierająca liczebności oczekiwane:
Obliczanie wartości oczekiwanych
| Płeć | Stosowanie kremu na zmarszczki | Ogółem | |
|---|---|---|---|
| Nie | Tak | ||
| Mężczyzna | 24,9 | 91,1 | 116 |
| Kobieta | 27,1 | 98,9 | 126 |
| Ogółem | 52 | 190 | 242 |
Czym jest liczebność oczekiwana?
Mówi ona ilu mężczyzn i ile kobiet powinno opowiedzieć się za, a ile przeciw stosowaniu kremu na zmarszczki.
Gdy już mamy liczebności empiryczne i oczekiwane, czas na wyliczenie chi 2.
Wzór na chi 2 jest następujący:
Z wzoru wynika, że aby obliczyć chi 2 potrzebujemy najpierw obliczyć różnice między liczebnościami empirycznymi i oczekiwanymi dla każdej komórki tabeli, będzie to nasze
Różnica liczebności empirycznych i oczekiwanych między mężczyznami stosującymi krem na zmarszczki wynosi 36-24,9=11,1
W poniższej tabeli znajduje się wyliczenie różnic między wartościami oczekiwanymi a empirycznie uzyskanymi.
Zestawienie liczebności empirycznych i oczekiwanych i różnic między nimi
| Płeć | Stosowanie kremu na zmarszczki | Ogółem | |||
|---|---|---|---|---|---|
| Nie | f0-fe | Tak | f0-fe | ||
| Mężczyzna - liczebności empiryczne (f0) | 36 | 11,1 | 80 | -11,1 | 116 |
| Mężczyzna - liczebnosci oczekiwane (fe) | 24,9 | 91,1 | |||
| Kobieta - liczebnosci empiryczne (f0) | 16 | -11,1 | 110 | 11,1 | 126 |
| Kobieta - liczebności oczekiwane (fe) | 27,1 | 98,9 | |||
| Ogółem | 52 | 190 | 242 | ||
Widzimy, że różnice między liczebnościami oczekiwanymi, a empirycznymi są równe 11,1.
Wartość chi2 wynosi
Jak rozumieć test chi2 ?
Gdy rośnie różnica między liczebnościami empirycznymi i oczekiwanymi, wzrasta też wartość chi2, co oznacza, że im wyższa jest wartość statystyki chi2, tym większe jest prawdopodobieństwo istnienia zależności między zmiennymi.
Przypomnijmy, że testujemy H0, która mówi, że nie ma istotnych różnic w stosowaniu kremu na zmarszczki między kobietami a mężczyznami.
Chi 2 wynosi 12,093. Musimy jeszcze wskazać poziom istotności oraz obliczyć liczbę stopni swobody .
Poziom istotności przyjmiemy 0,01.
Stopnie swobody wyliczamy ze wzoru df = (r-1)(c-1)
gdzie „r” to liczba wierszy, a „c” to liczba kolumn.
Liczba stopni swobody wynosi więc df=(2-1)(2-1)=1
Gdy mamy poziom istotności oraz wyliczone stopnie swobody, możemy porównać chi 2 uzyskane z obliczeń i chi 2 z rozkładu.
Wartość chi 2, przy poziomie istotności 0,01 i liczbie stopni swobody 1 wynosi 6,635. Tablice rozkładu wartości krytycznych rozkładu chi 2 można znaleźć tutaj
Uzyskana przez nas wartość chi 2 12,093 jest większa od teoretycznego 6,635, co stanowi podstawę do odrzucenia hipotezy zerowej.
Jak zapisać wynik?
X2 (1, N=242) = 12,093; p<0,01
Jak wynik wyglądałby w programie komputerowym SPSS?
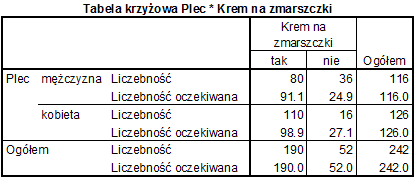
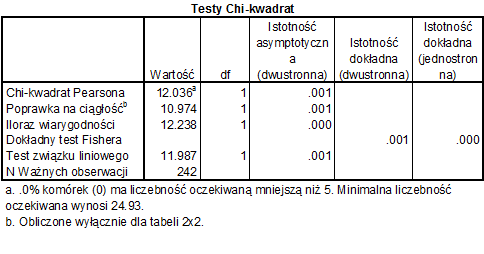
Jak widać, nie potrzebujesz niczego wyliczać. Program sam podaje statystykę chi2 oraz poziom istotności. Aby stwierdzić czy istnieje związek między dwiema zmiennymi wystarczy spojrzeć na powyższą tabelę, a dokładniej, na kolumnę „istotność asymptotyczna (dwustronna)”. Jeżeli wartość p jest mniejsza lub równa niż przyjęty przez nas poziom istotności, oznacza to, że istnieje zależność między zmiennymi.
W naszym przypadku test niezależności dwóch zmiennych chi2 jest istotny statystycznie, co oznacza, że hipotezę zerową, o braku związku między zmiennymi, należy odrzucić. Przyjmujemy hipotezę alternatywną, która mówi, że występuje istotny związek między analizowanymi zmiennymi.

